Model calibration

Data

Code 
plot_info <- read.csv("data/raw_data/bioforest-plot-information.csv") |>
  select(site, plot, Year_of_harvest, Treatment)

data <- read.csv("data/derived_data/aggregated_data_v9.csv") |>
  mutate(plot_new = Plot) |>
  separate(Plot, "Plot", "_") |>
  left_join(plot_info, by = join_by(Site == site, Plot == plot)) |>
  filter(grepl("^agb", variable)) |>
  pivot_wider(names_from = "variable", values_from = "value") |>
  mutate(prod = agb_growth + agb_recr, mort = agb_mort, stocks = agb) |>
  select(!contains("agb")) |>
  pivot_longer(cols = c("stocks", "prod", "mort"), names_to = "variable") |>
  mutate(Year_of_harvest = ifelse(Site == "Mbaiki" & Treatment == "Logging",
    1985, Year_of_harvest
  )) |>
  mutate(trec = Year - Year_of_harvest)

For now, we only calibrate the model with sites that meet all the criteria listed here, and that have at least 10 censuses.

Code 
sites <- read.csv("data/derived_data/sites_to_keep.csv") |>
  filter(ncensus >= 10)
data <- data |>
  filter(Site %in% sites$Site)

Model

We used the following parameter bounds when calibrating the model.

Code 
bounds <- data.frame(
  "theta_min" = 50,
  "theta_max" = 1000,
  "lambda_min" = 1e-2,
  "lambda_max" = 5,
  "alpha_min" = 0,
  "alpha_max" = 200,
  "delta_min" = 0,
  "delta_max" = 20,
  "tau_min" = 2,
  "tau_max" = 30,
  "omega_min" = 1e-3,
  "omega_max" = 0.5,
  "y0_min" = 10,
  "y0_max" = 1000
)
bounds |>
  pivot_longer(everything(), names_to = "parameter") |>
  separate(parameter, c("parameter", "bound")) |>
  pivot_wider(names_from = bound) |>
  flextable()

parameter

min

max

theta

50.000

1,000.0

lambda

0.010

5.0

alpha

0.000

200.0

delta

0.000

20.0

tau

2.000

30.0

omega

0.001

0.5

y0

10.000

1,000.0

Code 
data_rec <- data |>
  mutate(sitenum = as.numeric(as.factor(Site))) |>
  subset(Treatment == "Logging" & trec > 3) |>
  pivot_wider(names_from = "variable", values_from = "value") |>
  subset(!is.na(prod) & !is.na(mort)) |>
  mutate(plotnum = as.numeric(as.factor(paste(Site, plot_new))))
data_old <- data |>
  mutate(sitenum = as.numeric(as.factor(Site))) |>
  subset(Treatment == "Control" | trec < 0) |>
  pivot_wider(names_from = "variable", values_from = "value") |>
  subset(!is.na(prod) & !is.na(mort))
Code 
ind_rec <- data_rec |>
  select(Site, Plot, sitenum, plotnum) |>
  unique() |>
  arrange(plotnum)

mdata_all <- list(
  n_equ = nrow(data_old),
  n_log = nrow(data_rec),
  s = max(data_old$sitenum),
  p_log = max(data_rec$plotnum),
  y_equ = data_old$stocks,
  in_equ = data_old$prod,
  out_equ = data_old$mort,
  y_log = data_rec$stocks,
  in_log = data_rec$prod,
  out_log = data_rec$mort,
  time = data_rec$trec,
  site_equ = data_old$sitenum,
  site_log = data_rec$sitenum,
  plot_log = data_rec$plotnum,
  site_plot = ind_rec$sitenum,
  theta_bounds = c(bounds$theta_min, bounds$theta_max),
  lambda_bounds = c(bounds$lambda_min, bounds$lambda_max),
  alpha_bounds = c(bounds$alpha_min, bounds$alpha_max),
  delta_bounds = c(bounds$delta_min, bounds$delta_max),
  tau_bounds = c(bounds$tau_min, bounds$tau_max),
  omega_bounds = c(bounds$omega_min, bounds$omega_max),
  y0_bounds = c(bounds$y0_min, bounds$y0_max)
)
sample_model("flux_all", mdata_all)

The resulting Stan fit summary is presented below.

Code 
fit_flux_all <- as_cmdstan_fit(
  list.files("chains/flux_all/", full.names = TRUE)
)
fit_flux_all
 variable    mean  median    sd   mad      q5     q95 rhat ess_bulk ess_tail
 lp__     7039.36 7031.27 78.60 82.12 6928.00 7181.21 1.35        9       26
 mu_y0     355.39  354.87  6.18  6.66  346.58  366.01 1.07       44      441
 sigma_y0   19.72   19.65  0.52  0.46   18.92   20.62 1.02     1149     1637
 y0_p[1]   373.63  372.63 14.30 15.00  352.71  398.15 1.03       89     1564
 y0_p[2]   349.68  348.19 13.89 12.35  326.38  373.04 1.02      218      367
 y0_p[3]   338.83  339.91 13.63 13.03  314.71  360.31 1.02      214      621
 y0_p[4]   358.32  356.63 13.36 12.34  336.40  381.53 1.03      650     1493
 y0_p[5]   350.10  349.98 15.20 17.22  329.15  376.08 1.05       53      424
 y0_p[6]   350.93  351.35 15.64 17.19  327.90  377.04 1.06       40      271
 y0_p[7]   323.11  324.72 14.00 13.01  295.73  343.77 1.13       21       12

 # showing 10 of 7128 rows (change via 'max_rows' argument or 'cmdstanr_max_rows' option)
Code 
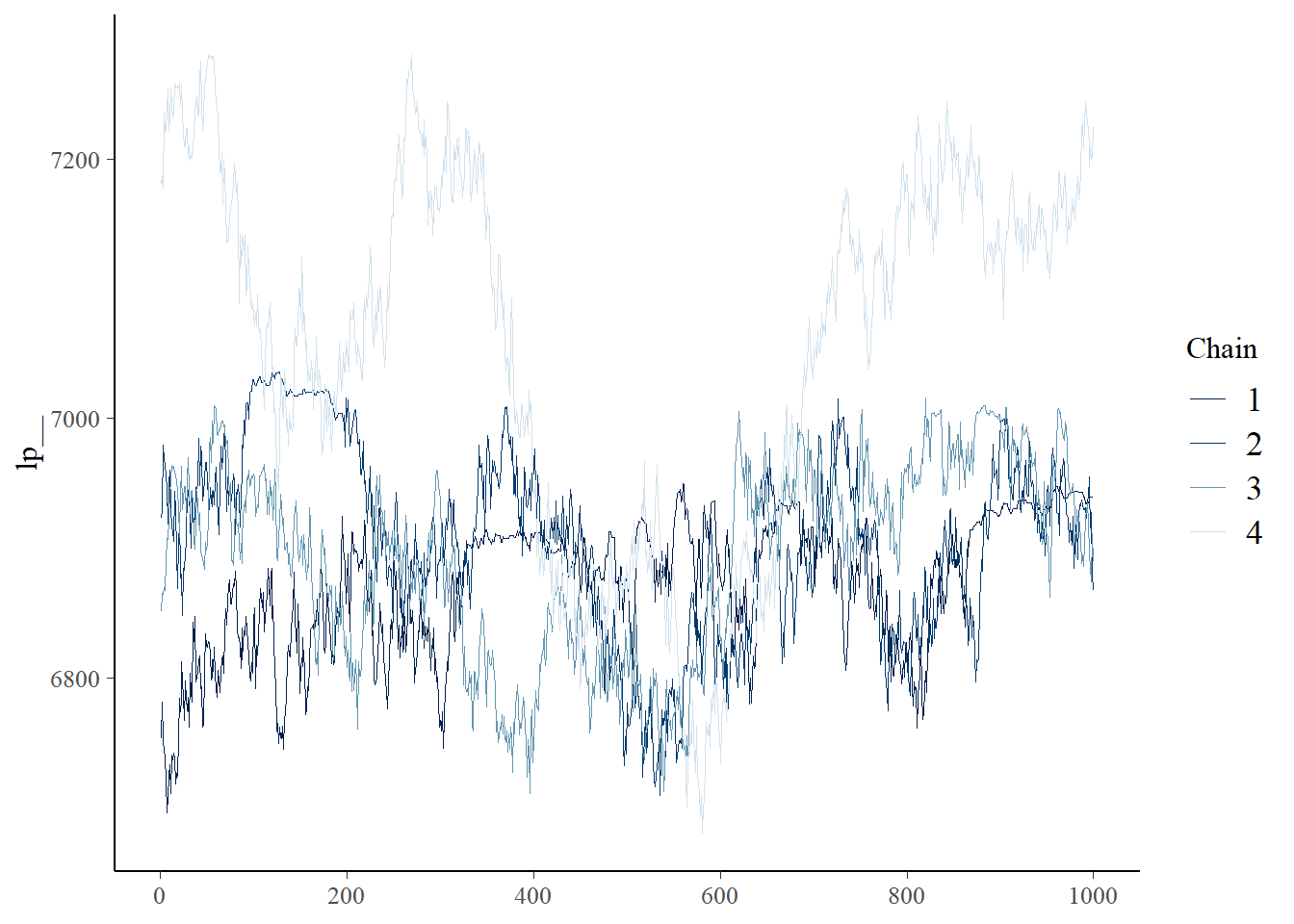
mcmc_trace(fit_flux_all$draws(variables = c("lp__")))

The main parameter values are consistent with our expectations.

Code 
c("lambda_s", "tau_s", "theta_s", "omega_s") |>
  fit_flux_all$summary() |>
  separate(variable, c("variable", NA, "sitenum")) |>
  mutate(sitenum = as.numeric(sitenum)) |>
  left_join(unique(data_old[, c("sitenum", "Site")])) |>
  select(variable, Site, mean, median, q5, q95, rhat)
# A tibble: 32 × 7
   variable Site           mean median    q5   q95  rhat
   <chr>    <chr>         <dbl>  <dbl> <dbl> <dbl> <dbl>
 1 lambda   Corinto       1.82   1.81  1.53  2.16   1.04
 2 lambda   Lesong        0.868  0.862 0.797 0.950  1.13
 3 lambda   Mbaiki        1.70   1.70  1.53  1.86   1.04
 4 lambda   Paracou       1.59   1.58  1.42  1.72   1.09
 5 lambda   SUAS          4.72   4.79  4.15  4.99   1.09
 6 lambda   Sungai Lalang 0.788  0.786 0.734 0.846  1.09
 7 lambda   Tapajos Km67  1.30   1.30  1.19  1.39   1.06
 8 lambda   Ulu Muda      0.835  0.829 0.776 0.900  1.03
 9 tau      Corinto       4.82   4.85  3.74  5.90   1.04
10 tau      Lesong        7.62   7.61  6.95  8.20   1.04
# ℹ 22 more rows

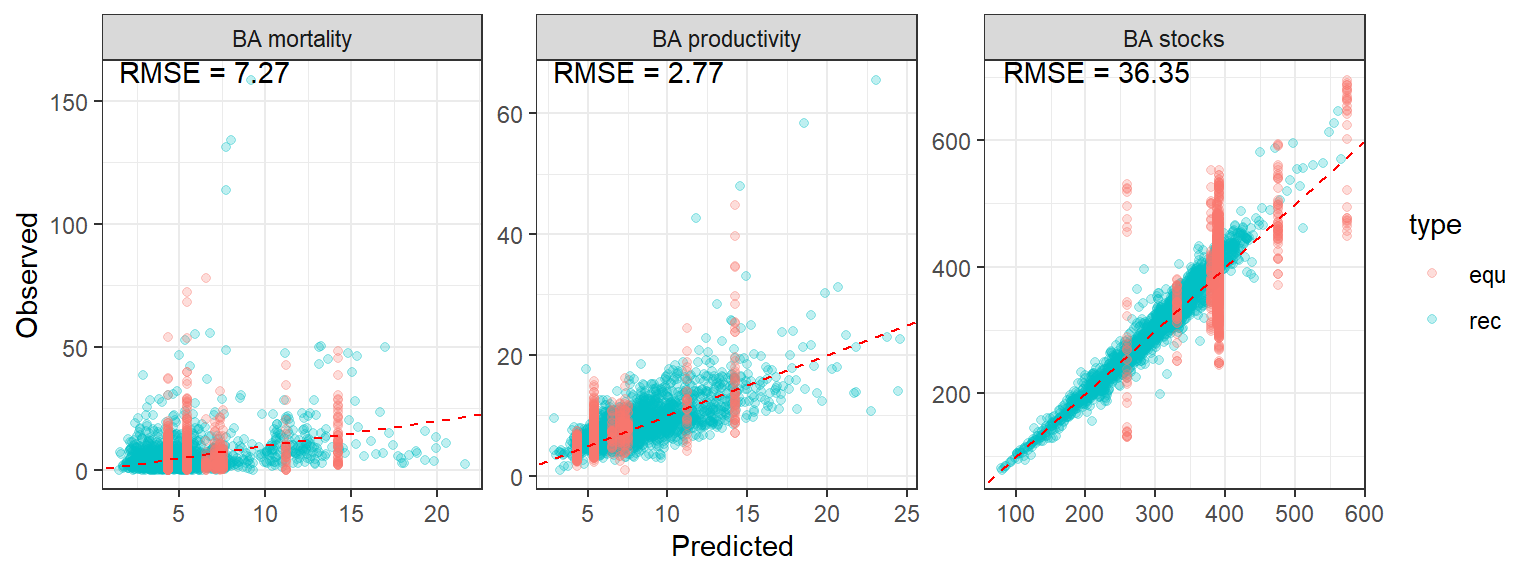
The goodness of fit is satisfactory.

Code 
pred_data <- data_rec |>
  select(-plotnum) |>
  mutate(
    stocks = fit_flux_all$summary(c("mu_y_log"), median)$median,
    prod = fit_flux_all$summary(c("mu_in_log"), median)$median,
    mort = fit_flux_all$summary(c("mu_out_log"), median)$median,
    val = "pred",
    type = "rec"
  ) |>
  rbind(mutate(
    data_old,
    stocks =
      fit_flux_all$summary(c("theta_s"), median)$median[data_old$sitenum],
    prod = fit_flux_all$summary(c("theta_s"), median)$median[data_old$sitenum] *
      fit_flux_all$summary(c("omega_s"), median)$median[data_old$sitenum], # nolint
    mort = fit_flux_all$summary(c("theta_s"), median)$median[data_old$sitenum] *
      fit_flux_all$summary(c("omega_s"), median)$median[data_old$sitenum], # nolint
    val = "pred",
    type = "equ"
  ))

obs_data <- data_rec |>
  mutate(
    val = "obs",
    type = "rec"
  ) |>
  select(-plotnum) |>
  rbind(mutate(
    data_old,
    val = "obs",
    type = "equ"
  ))

pov_data <- rbind(pred_data, obs_data) |>
  pivot_longer(cols = c(stocks, prod, mort), names_to = "variable") |>
  pivot_wider(names_from = val, values_from = value)

df_rmse <- pov_data |>
  group_by(variable) |>
  summarise(rmse = sqrt(mean((pred - obs)^2)))

labs <- c(stocks = "BA stocks", prod = "BA productivity", mort = "BA mortality")

pov_data |>
  ggplot(aes(pred, obs)) +
  geom_point(alpha = 0.25, aes(col = type)) +
  geom_abline(col = "red", linetype = "dashed") +
  geom_text(
    data = df_rmse,
    aes(
      x = -Inf, y = Inf, hjust = -0.1, vjust = 1,
      label = paste("RMSE =", round(rmse, 2))
    )
  ) +
  theme_bw() +
  xlab("Predicted") +
  ylab("Observed") +
  facet_wrap(~variable, scales = "free", labeller = labeller(variable = labs))

Predicted vs observed values.

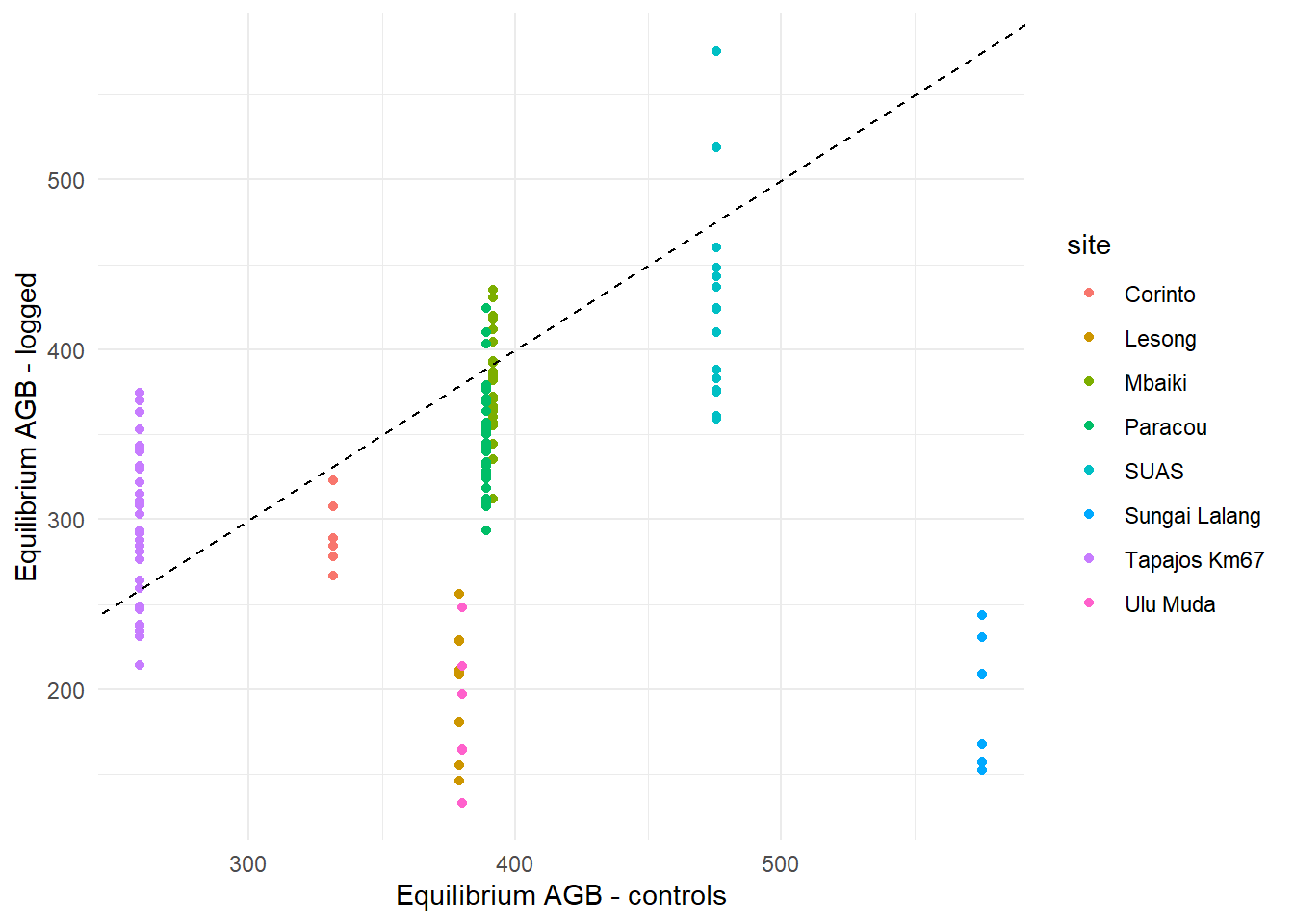
The equilibrium AGB estimated in the logged plots is consistent overall with the control plots, except in the Malaysian sites (Lesong, Sungai Lalang and Ulu Muda), where it is significantly lower.

Code 
ind_rec <- data_rec |>
  select(Site, Plot, sitenum, plotnum) |>
  unique() |>
  arrange(plotnum)
data.frame(
  site = levels(as.factor(data_old$Site))[ind_rec$sitenum],
  theta_rec = fit_flux_all$summary(c("theta_log"), median)$median,
  theta_equ =
    fit_flux_all$summary(c("theta_s"), median)$median[ind_rec$sitenum]
) |>
  ggplot(aes(theta_equ, theta_rec, col = site)) +
  geom_point() +
  geom_abline(intercept = 0, slope = 1, lty = 2) +
  labs(x = "Equilibrium AGB - controls", y = "Equilibrium AGB - logged") +
  theme_minimal()

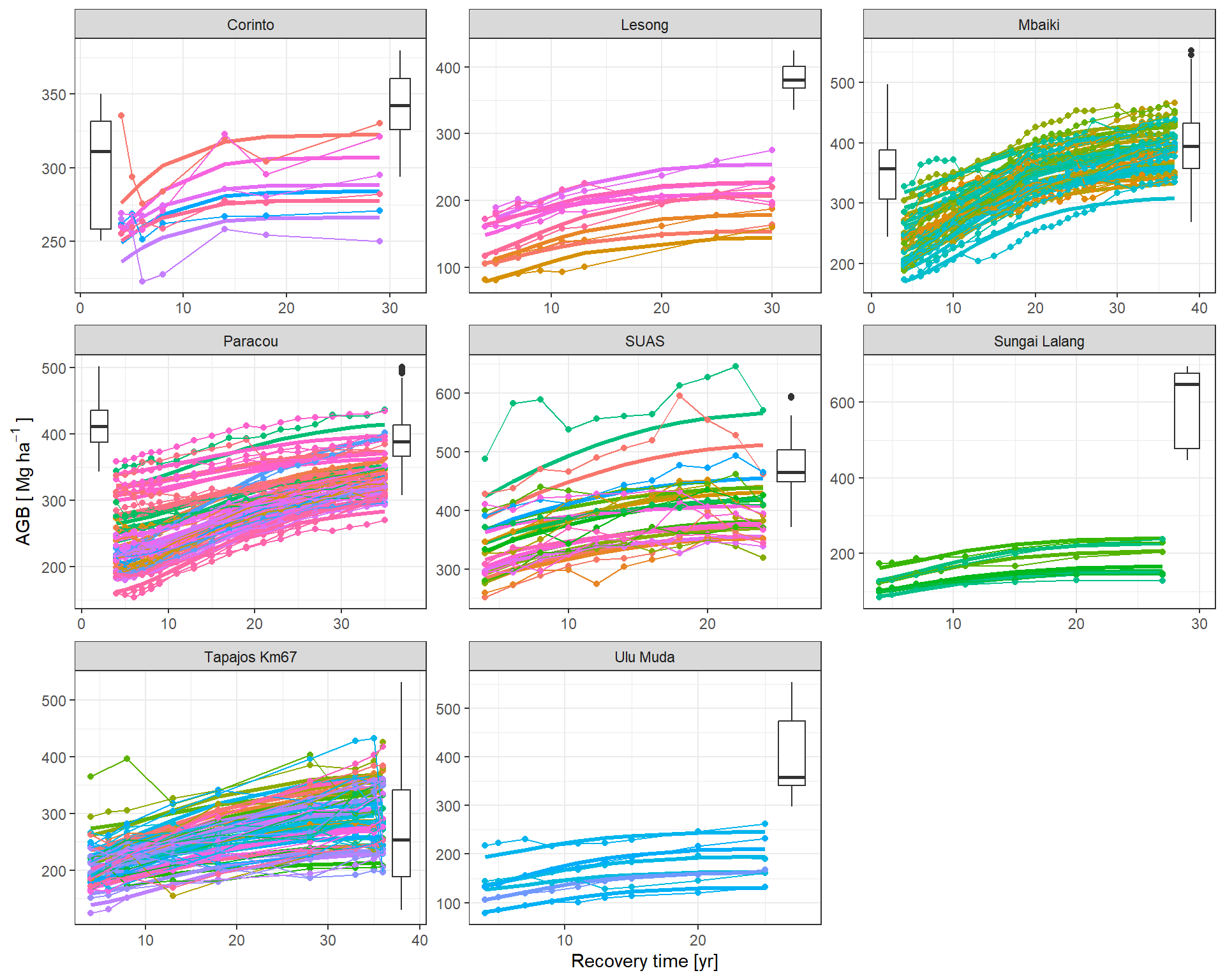
Visualising the trajectories

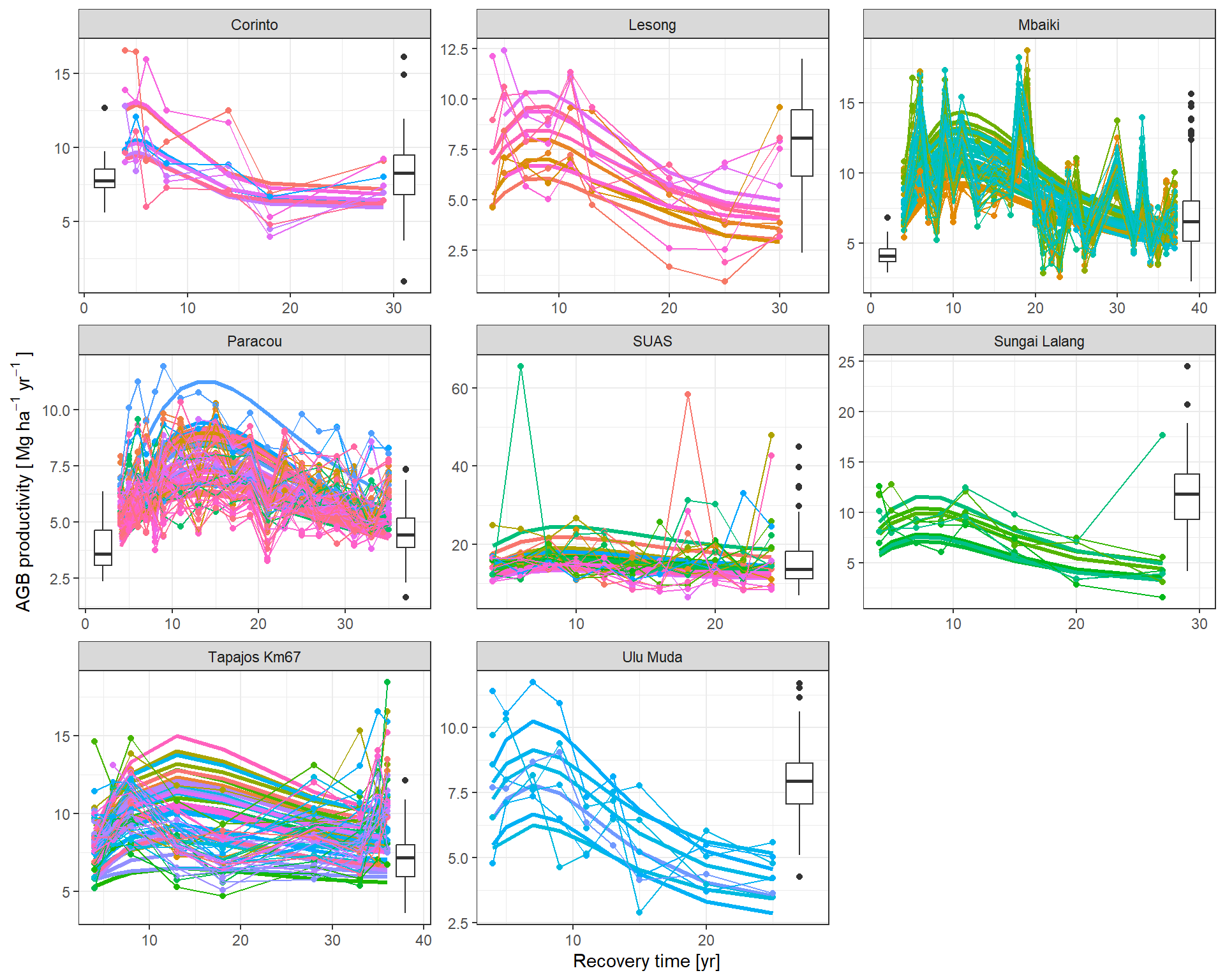
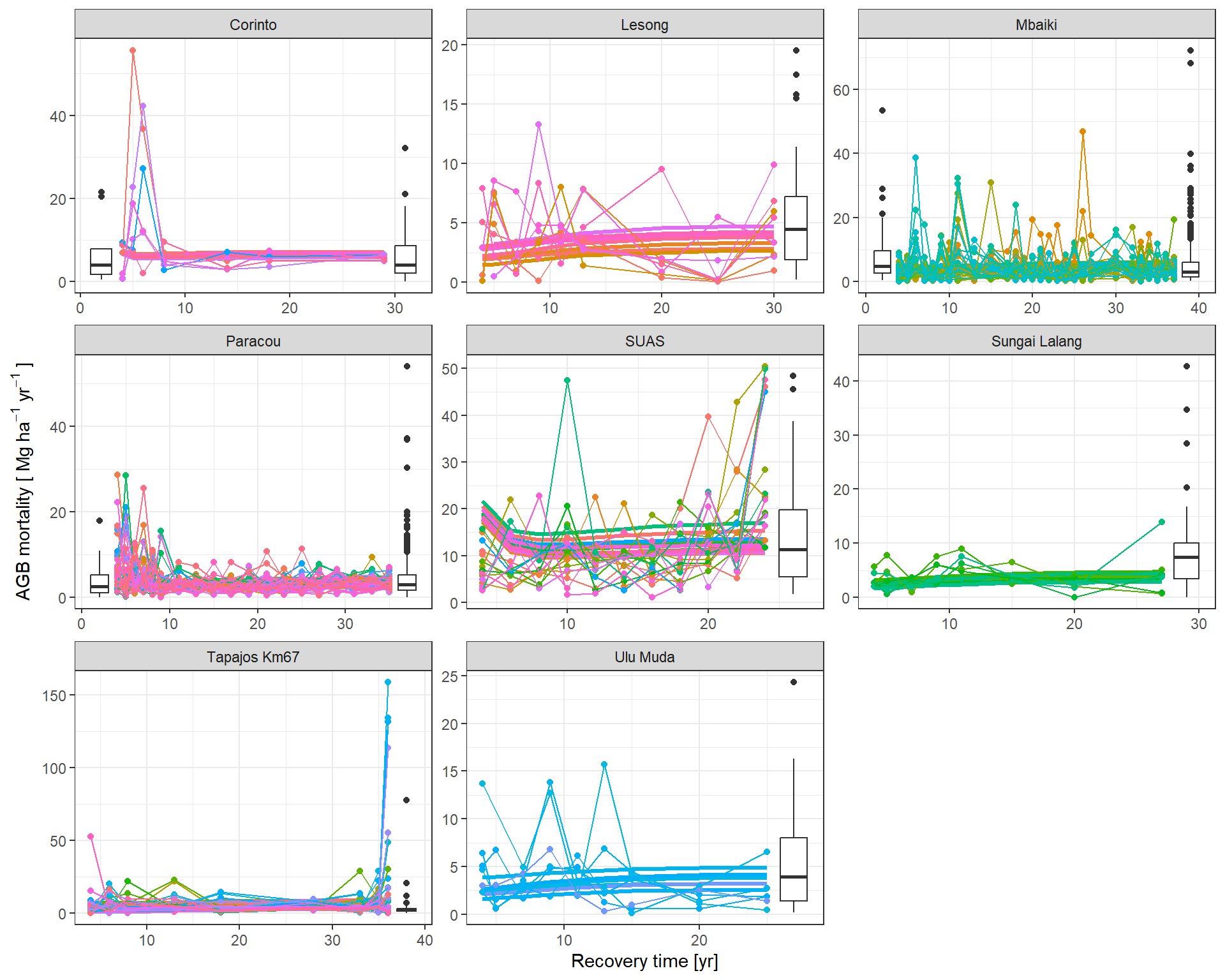
The predicted flux and stocks trajectories look consistent with the data.

Code 
pov_data |>
  subset(variable == "stocks") |>
  mutate(Plot = plot_new) |>
  graph_traj(expression("AGB [" ~ Mg ~ ha^-1 ~ "]"))

Predicted trajectories.
Code 
pov_data |>
  subset(variable == "prod") |>
  mutate(Plot = plot_new) |>
  graph_traj(expression("AGB productivity [" ~ Mg ~ ha^-1 ~ yr^-1 ~ "]"))

Predicted trajectories.
Code 
pov_data |>
  subset(variable == "mort") |>
  mutate(Plot = plot_new) |>
  graph_traj(expression("AGB mortality [" ~ Mg ~ ha^-1 ~ yr^-1 ~ "]"))

Predicted trajectories.