Composition change data

Formula for the contribution of fluxes

The contribution of a given flux (recruitment, growth or mortality) at time \(t\) can be written as:

\[CF_{F,t} = \sum_{i\in F_t}\frac{ba_{i,t} (ft_{i} - CWM_{t-1})}{BA_{t}}-\sum_{i\in F_t}\frac{ba_{i,t-1} (ft_{i} - CWM_{t-1})}{BA_{t-1}}\] where \(F_t\) is the set of trees contributing to a given flux between \(t-1\) and \(t\) (recruitment: trees recruited at \(t\); growth: trees that were measured and alive at \(t\) and \(t-1\); mortality: trees that died between \(t-1\) and \(t\)).

\(ba_{i,t}\) is the basal area of a tree \(i\) at time \(t\); \(ft_{i}\) is the functional trait value of tree \(i\); \(BA_t\) is the basal area of the entire community at \(t\); \(CWM_t\) is the community weighted mean trait value at \(t\).

We subtract \(CWM_{t-1}\) to have negative contributions when the flux decreases the CWM between \(t-1\) and \(t\); and positive contributions that increase the \(CWM\).

As written, the contributions are additive:

\[CWM_t= CWM_{t-1} + CF_{G,t} + CF_{R,t}+CF_{M,t}\]

Data

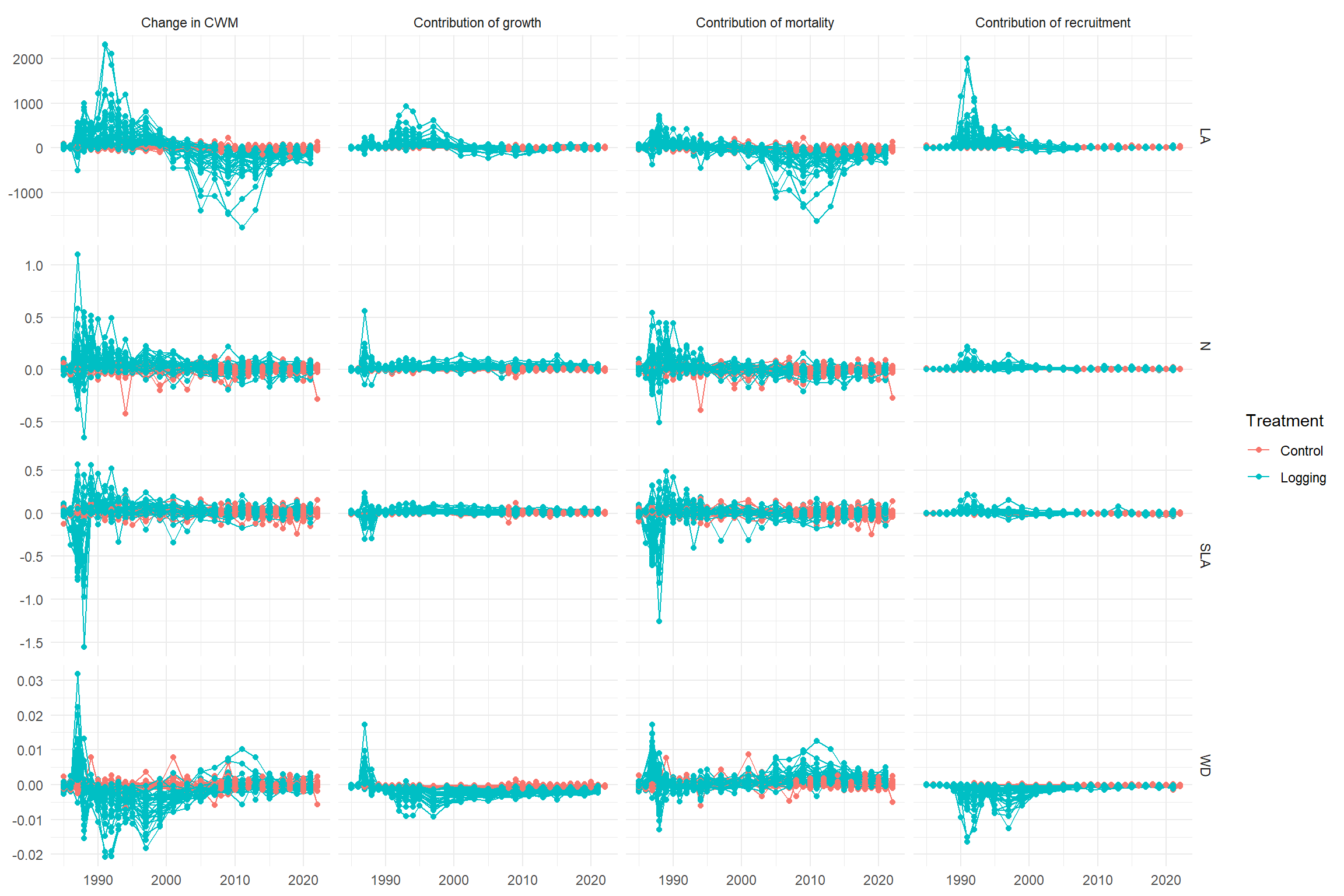
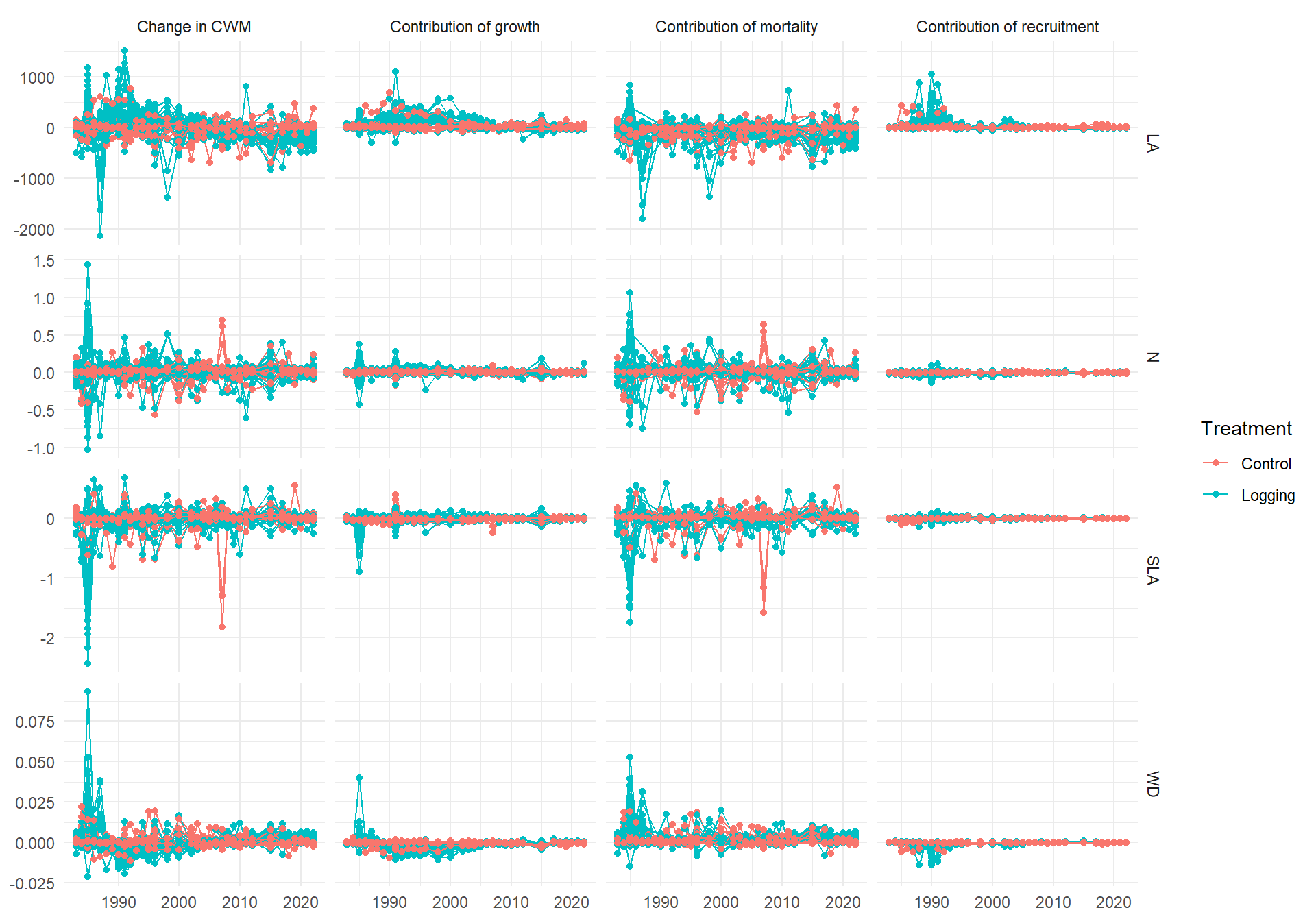
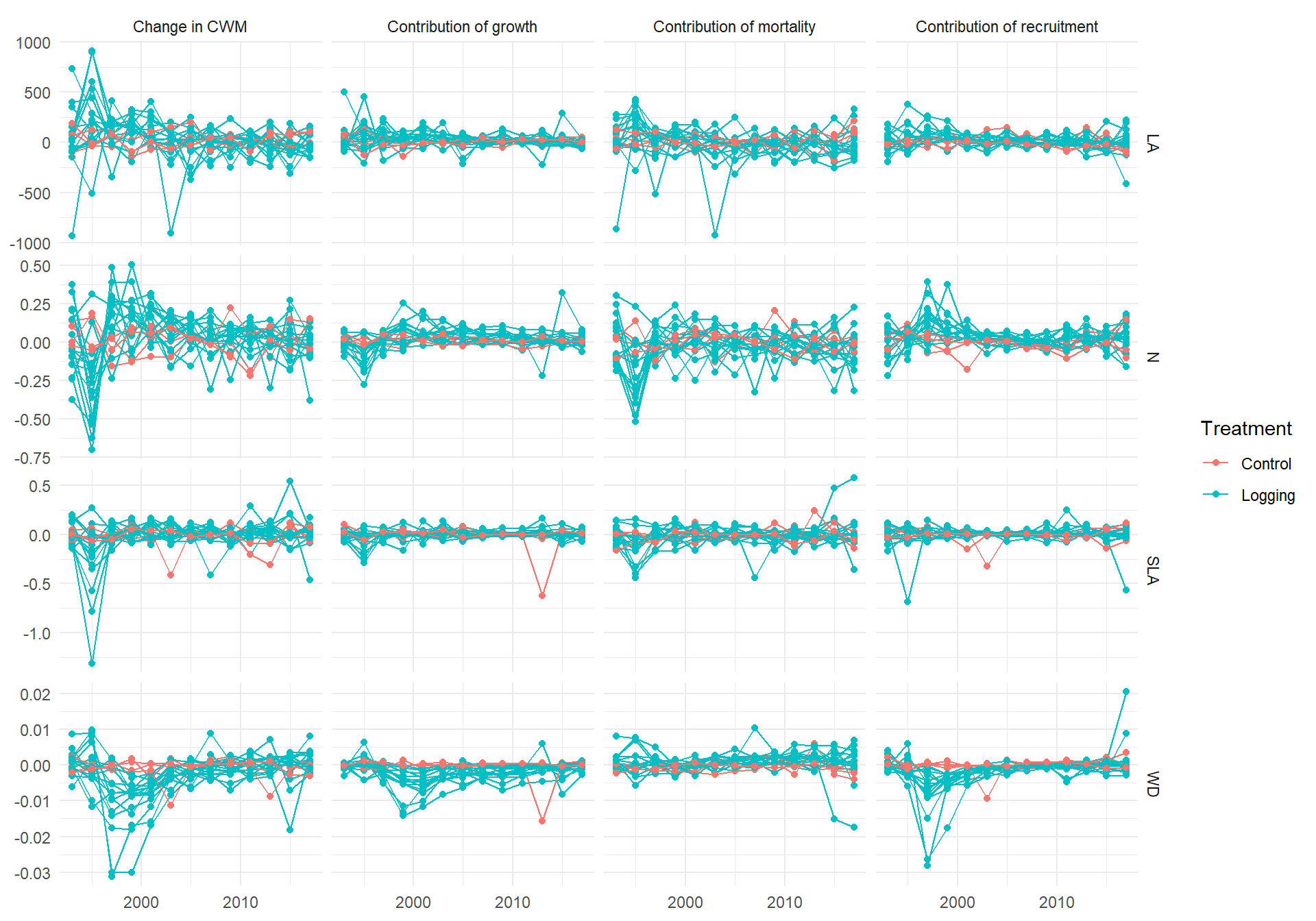
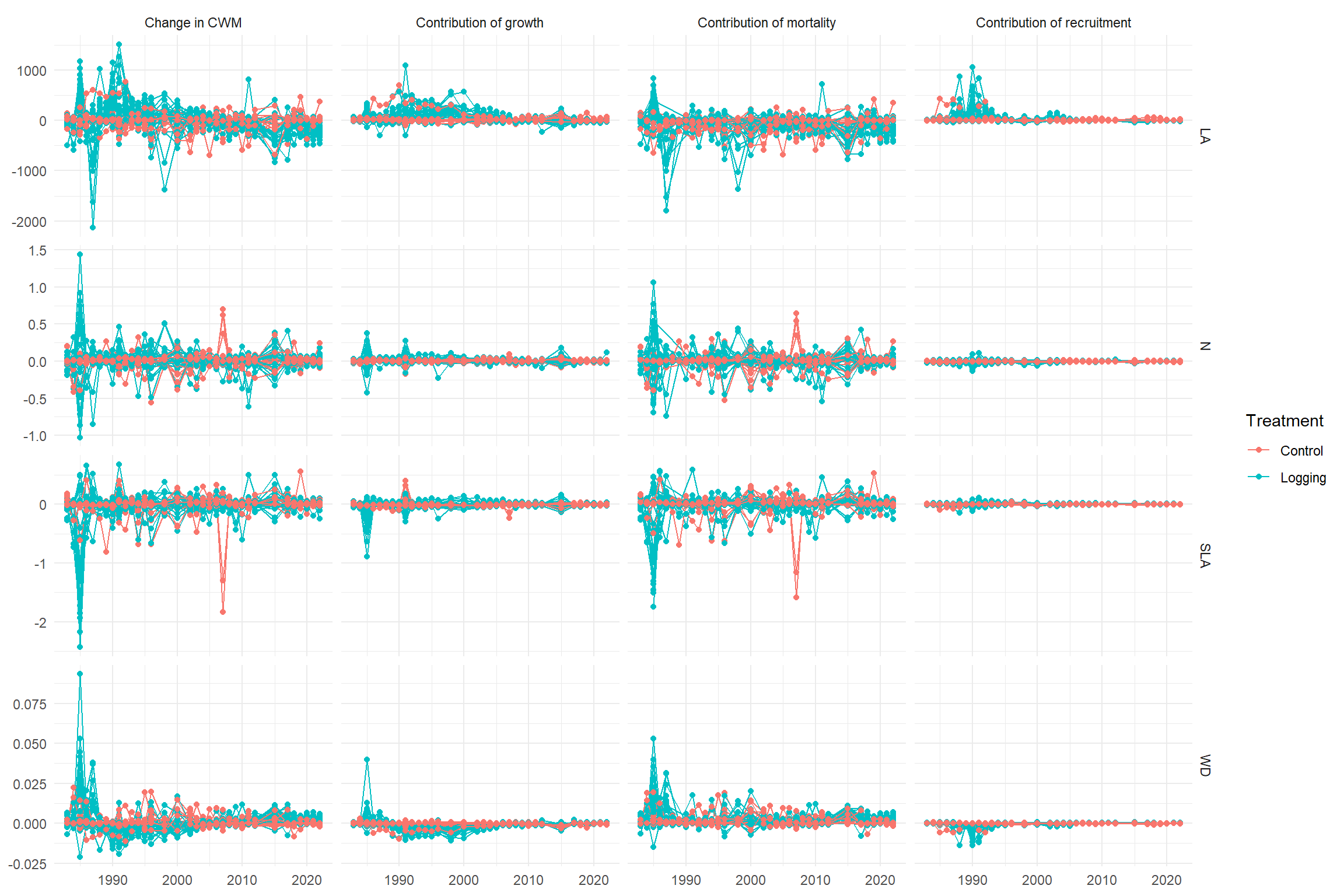
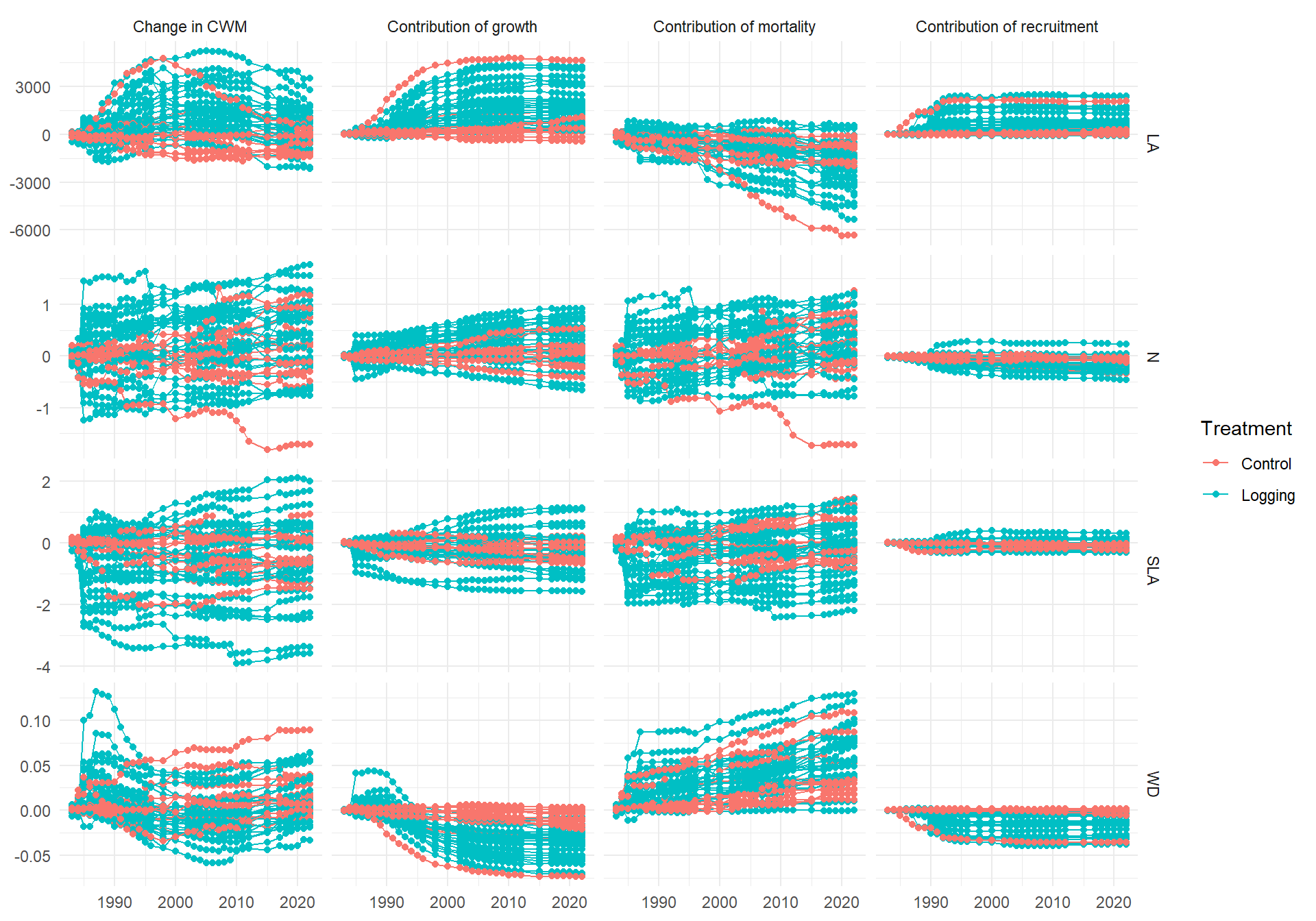
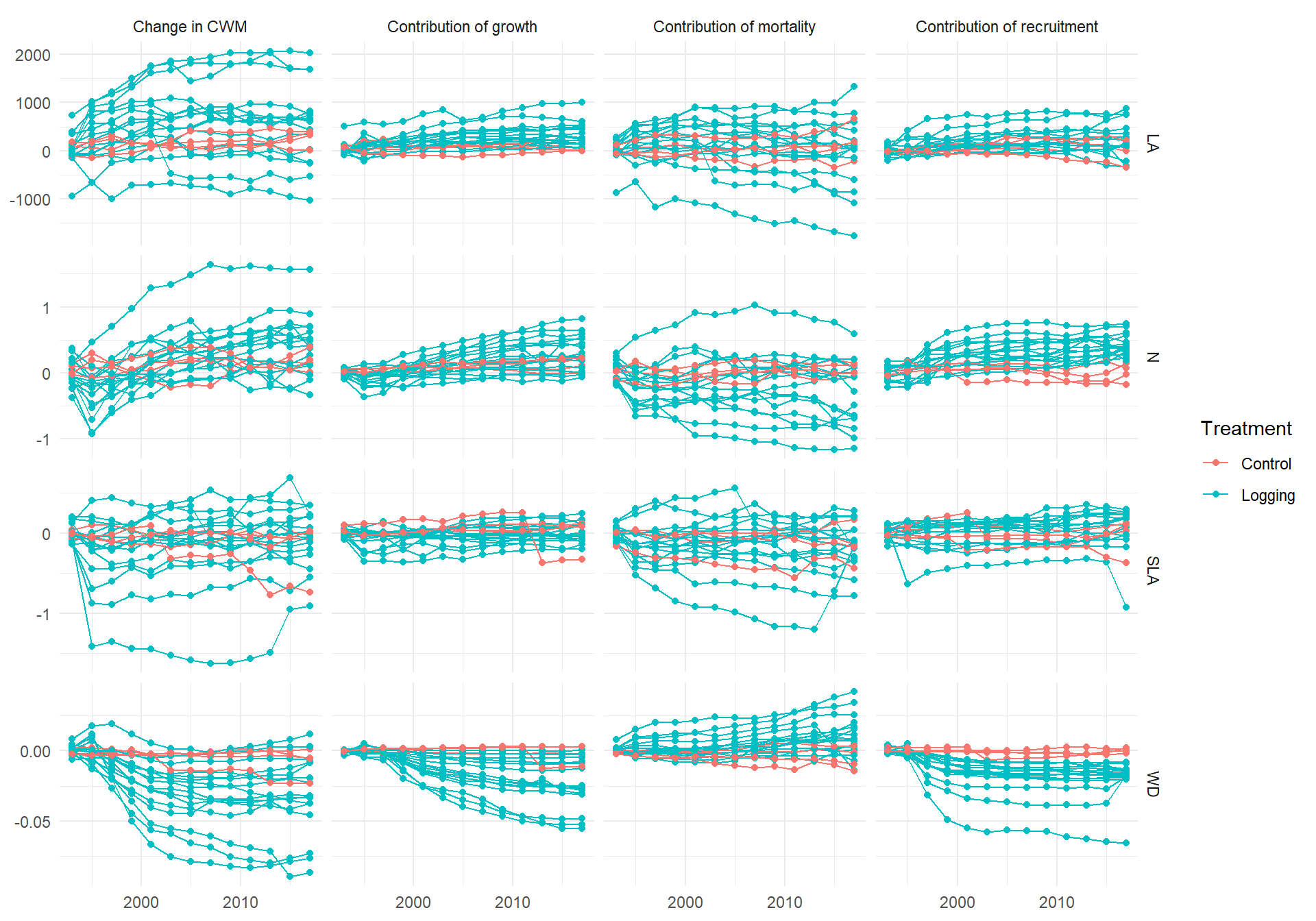
Code

plot_info <- read.csv("data/raw_data/bioforest-plot-information.csv") |>
  select(site, plot, Year_of_harvest, Treatment)
data <- read.csv("data/derived_data/aggregated_data_v9.csv") |>
  mutate(plot_new = Plot) |>
  separate(Plot, "Plot", "_") |>
  left_join(plot_info, by = join_by(Site == site, Plot == plot)) |>
  filter(grepl("cwmdiff", variable)) |>
  separate(variable, c("trait", NA, "flux"), sep = "_")

Annual changes

Code

labs_flux <- c(
  all = "Change in CWM",
  rba = "Contribution of recruitment",
  gba = "Contribution of growth",
  mba = "Contribution of mortality"
)
data |>
  filter(Site == "Paracou") |>
  ggplot(aes(x = Year, y = value, group = plot_new, col = Treatment)) +
  geom_line() +
  geom_point() +
  facet_grid(trait ~ flux,
    scales = "free",
    labeller = labeller(flux = labs_flux)
  ) +
  labs(y = NULL, x = NULL) +
  theme_minimal()

Code

labs_flux <- c(
  all = "Change in CWM", rba = "Contribution of recruitment",
  gba = "Contribution of growth",
  mba = "Contribution of mortality"
)
data |>
  filter(Site == "Mbaiki") |>
  ggplot(aes(x = Year, y = value, group = plot_new, col = Treatment)) +
  geom_line() +
  geom_point() +
  facet_grid(trait ~ flux,
    scales = "free",
    labeller = labeller(flux = labs_flux)
  ) +
  labs(y = NULL, x = NULL) +
  theme_minimal()

Code

labs_flux <- c(
  all = "Change in CWM", rba = "Contribution of recruitment",
  gba = "Contribution of growth",
  mba = "Contribution of mortality"
)
data |>
  filter(Site == "SUAS") |>
  ggplot(aes(x = Year, y = value, group = plot_new, col = Treatment)) +
  geom_line() +
  geom_point() +
  facet_grid(trait ~ flux,
    scales = "free",
    labeller = labeller(flux = labs_flux)
  ) +
  labs(y = NULL, x = NULL) +
  theme_minimal()

Cumulative changes

Code

labs_flux <- c(
  all = "Change in CWM",
  rba = "Contribution of recruitment",
  gba = "Contribution of growth",
  mba = "Contribution of mortality"
)
data |>
  filter(Site == "Paracou") |>
  arrange(Site, plot_new, Year) |>
  group_by(Site, plot_new, trait, flux) |> 
  mutate(value_cum = cumsum(value)) |> 
  ggplot(aes(x = Year, y = value_cum, group = plot_new, col = Treatment)) +
  geom_line() +
  geom_point() +
  facet_grid(trait ~ flux,
    scales = "free",
    labeller = labeller(flux = labs_flux)
  ) +
  labs(y = NULL, x = NULL) +
  theme_minimal()

Code

labs_flux <- c(
  all = "Change in CWM", rba = "Contribution of recruitment",
  gba = "Contribution of growth",
  mba = "Contribution of mortality"
)
data |>
  filter(Site == "Mbaiki") |>
  arrange(Site, plot_new, Year) |>
  group_by(Site, plot_new, trait, flux) |> 
  mutate(value_cum = cumsum(value)) |> 
  ggplot(aes(x = Year, y = value_cum, group = plot_new, col = Treatment)) +
  geom_line() +
  geom_point() +
  facet_grid(trait ~ flux,
    scales = "free",
    labeller = labeller(flux = labs_flux)
  ) +
  labs(y = NULL, x = NULL) +
  theme_minimal()

Code

labs_flux <- c(
  all = "Change in CWM", rba = "Contribution of recruitment",
  gba = "Contribution of growth",
  mba = "Contribution of mortality"
)
data |>
  filter(Site == "SUAS") |>
  arrange(Site, plot_new, Year) |>
  group_by(Site, plot_new, trait, flux) |> 
  mutate(value_cum = cumsum(value)) |> 
  ggplot(aes(x = Year, y = value_cum, group = plot_new, col = Treatment)) +
  geom_line() +
  geom_point() +
  facet_grid(trait ~ flux,
    scales = "free",
    labeller = labeller(flux = labs_flux)
  ) +
  labs(y = NULL, x = NULL) +
  theme_minimal()